What is the time period the for planets to orbit the star

Boosted reading at www.astronomynotes.com

• Kepler's laws of planetary motion

---

Elliptical path of planet orbiting the Sun

Offset Law

Kepler was a sophisticated mathematician, and so the advance that he made in the written report of the motion of the planets was to introduce a mathematical foundation for the heliocentric model of the solar organisation. Where Ptolemy and Copernicus relied on assumptions, such as that the circle is a "perfect" shape and all orbits must exist round, Kepler showed that mathematically a circular orbit could non lucifer the data for Mars, but that an elliptical orbit did match the data! Nosotros now refer to the following argument as Kepler's First Police:

• The planets orbit the Sun in ellipses with the Sun at one focus (the other focus is empty).

For more than information about ellipses, you can read in gory mathematical detail the page hosted at Mathworld, and at that place is also information on ellipses in Wikipedia.

Hither is a demonstration of the classic method for drawing an ellipse:

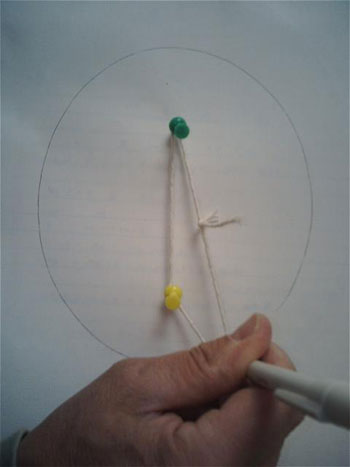
The archetype method for cartoon an ellipse using a loop of string effectually two tacks separated by a small distance.

The ii thumbtacks in the image stand for the two foci of the ellipse, and the string ensures that the sum of the distances from the ii foci (the tacks) to the pencil is a constant. Beneath is another image of an ellipse with the major centrality and minor axis defined:

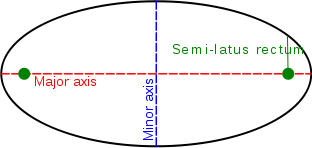
Diagram of a cartoon of an ellipse, showing definition of major and modest axes and foci.

We know that in a circumvolve, all lines that laissez passer through the center (diameters) are exactly equal in length. Yet, in an ellipse, lines that you depict through the center vary in length. The line that passes from one terminate to the other and includes both foci is called the major axis, and this is the longest distance between two points on the ellipse. The line that is perpendicular to the major axis at its center is called the minor axis, and it is the shortest altitude betwixt two points on the ellipse.

In the image above, the green dots are the foci (equivalent to the tacks in the photo above). The larger the distance between the foci, the larger the eccentricity of the ellipse. In the limiting example where the foci are on top of each other (an eccentricity of 0), the figure is actually a circumvolve. So you can think of a circle equally an ellipse of eccentricity 0. Studies have shown that astronomy textbooks introduce a misconception by showing the planets' orbits as highly eccentric in an effort to be sure to bulldoze home the point that they are ellipses and non circles. In reality the orbits of nearly planets in our Solar System are very close to circular, with eccentricities of near 0 (e.g., the eccentricity of Earth's orbit is 0.0167). For an animation showing orbits with varying eccentricities, see the eccentricity diagram at "Windows to the Universe." Note that the orbit with an eccentricity of 0.two, which appears nearly circular, is similar to Mercury's, which has the largest eccentricity of whatever planet in the Solar Organization. The elliptical orbits diagram at "Windows to the Universe" includes an paradigm with a direct comparison of the eccentricities of several planets, an asteroid, and a comet. Note that if you follow the Starry Nighttime instructions on the previous page to detect the orbits of Earth and Mars from above, yous can also see the shapes of these orbits and how circular they appear.

Kepler's first law has several implications. These are:

• The distance between a planet and the Lord's day changes as the planet moves along its orbit.
• The Lord's day is kickoff from the center of the planet's orbit.

2d Law

In their models of the Solar System, the Greeks held to the Aristotelian belief that objects in the sky moved at a constant speed in circles considering that is their "natural motion." However, Kepler's 2d law (sometimes referred to as the Law of Equal Areas), tin exist used to show that the velocity of a planet changes as it moves along its orbit!

Kepler'southward 2d police force is:

• The line joining the Dominicus and a planet sweeps through equal areas in an equal corporeality of time.

The image beneath links to an animation that demonstrates that when a planet is well-nigh aphelion (the point furthest from the Sun, labeled with a B on the screen grab beneath) the line drawn betwixt the Sun and the planet traces out a long, skinny sector between points A and B. When the planet is close to perihelion (the bespeak closest to the Sun, labeled with a C on the screen grab beneath), the line drawn between the Sun and the planet traces out a shorter, fatter sector between points C and D. These slices that alternating greyness and blue were drawn in such a mode that the area within each sector is the same. That is, the sector between C and D on the correct contains the same amount of area every bit the sector between A and B on the left.

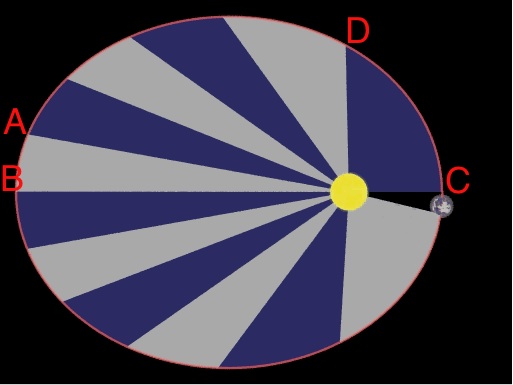
Click on this prototype to launch the animation in Windows Media Thespian. It shows a planet sweeping out equal areas in equal times.
Kepler's 2nd Police force

Credit: Dr. Michael Gallis, Penn Country Schuylkill

Since the areas of these two sectors are identical, then Kepler's 2nd law says that the time information technology takes the planet to travel between A and B and also between C and D must be the aforementioned. If you look at the altitude along the ellipse betwixt A and B, it is shorter than the distance between C and D. Since velocity is distance divided past time, and since the altitude between A and B is shorter than the distance betwixt C and D, when y'all divide those distances by the aforementioned amount of time y'all find that:

• A planet is moving faster virtually perihelion and slower near aphelion.

The orbits of well-nigh planets are well-nigh circular, with eccentricities nigh 0. In this case, the changes in their speed are not as well large over the grade of their orbit.

For those of you who teach physics, you might annotation that really, Kepler'due south second law is just another way of stating that angular momentum is conserved. That is, when the planet is near perihelion, the distance between the Sun and the planet is smaller, and then it must increment its tangential velocity to conserve athwart momentum, and similarly, when information technology is near aphelion when their separation is larger, its tangential velocity must subtract so that the total orbital athwart momentum is the same equally it was at perihelion.

Tertiary Law

Kepler had all of Tycho'southward information on the planets, then he was able to make up one's mind how long each planet took to complete ane orbit around the Dominicus. This is usually referred to equally the menses of an orbit. Kepler noted that the closer a planet was to the Sunday, the faster it orbited the Sun. He was the showtime scientist to study the planets from the perspective that the Sun influenced their orbits. That is, different Ptolemy and Copernicus, who both assumed that the planet's "natural move" was to move at abiding speeds along round paths, Kepler believed that the Sun exerted some kind of strength on the planets to push them along their orbits, and because of this, the closer they are to the Sun, the faster they should move.

Kepler studied the periods of the planets and their distance from the Dominicus, and proved the following mathematical relationship, which is Kepler's Third Law:

• The square of the period of a planet's orbit (P) is directly proportional to the cube of the semimajor centrality (a) of its elliptical path.

• $P^2\propto a^3$

What this ways mathematically is that if the foursquare of the period of an object doubles, and then the cube of its semimajor axis must as well double. The proportionality sign in the above equation ways that:

• $P^2=k{a}^3$

where k is a abiding number. If we divide both sides of the equation by $a^{\mathrm{three}}$ , we see that:

• $P^2/a^3=k$

This means that for every planet in our solar system, the ratio of their period squared to their semimajor axis cubed is the same constant value, so this means that:

• $\left(P^2/a^{\mathrm{iii}}\right){}_{Earth}=\left(P^2/a^3\right){}_{Mar\mathrm{southward}}=\left(P^2/a^{\mathrm{three}}\right){}_{Jupiter}$

We know that the menses of the Globe is 1 yr. At the fourth dimension of Kepler, they did not know the distances to the planets, but we can simply assign the semimajor axis of the Earth to a unit we call the Astronomical Unit (AU). That is, without knowing how big an AU is, we simply fix $a_{Earth}=1AU$ . If y'all plug 1 twelvemonth and 1 AU into the equation above, you lot see that:

• $\left(P^2/a^{\mathrm{iii}}\right){}_{Earth}=\left(P^2/a^3\right){}_{Mars}=\left(P^2/a^{\mathrm{three}}\right){}_{Jupiter}$

And then for every planet, $P^2/a^3=1$ if P is expressed in years and a is expressed in AU. So if you desire to calculate how far Saturn is from the Sun in AU, all you need to know is its period. For Saturn, this is approximately 29 years. And then:

• $\left(P^{\mathrm{ii}}/a^3\right){}_{Satur\mathrm{due\; north}}={\left(29years\right)}^{\mathrm{two}}/{\left(aAU\right)}^{\mathrm{three}}=1$
• ${\left(aAU\right)}^3=841$
• ${\text{(a AU) =}}^{\text{iii}}\surd \text{ 841 = 9.4 AU}$

So Saturn is 9.4 times further from the Sunday than the Earth is from the Sun!

hammersthroking.blogspot.com

Source: https://www.e-education.psu.edu/astro801/content/l2_p5.html

Share this post